"If I had only known, I would have been a locksmith." Albert Einstein
brainelevator a Joeybee philix production 2008 - 2024 stephen langton goulet
Welcome aboard.
What follows is an introduction to the original number and measure system responsible
for the design and construction of the Great Pyramid at Gizeh.
If a curiosity for archaeology, pyramidology, numbers, geometry, architecture, cosmology,
astronomy, phi, pi or simply coincidence brought you here, be assured. I have no axe
to grind, no con or hustle, no obligatory leap of faith, nothing to sell and
regrettably, no sexy cult to draw you in with.
You will face little more complexity than square roots, powers, ratios, scale and some
eight decimal numbers, so arm yourself accordingly and don't simply take my words.
The dimensions are the message. Confirm and learn them as you go, rather than
rushing through to the end in a frantic search for the "gist".
It's there. I just didn't put much into it.
On a skill level, any competently schooled grade eight arithmetic student
with a calculator, and some focus, will manage the math.
I am aware, there is enough speculation written and truths claimed about the Great Pyramid
over the previous five thousand years to pile up several word pyramids of equal size
around it. Despite an astonishing level of creative and intellectual output, absent
the original system of numbers and unit of measure applied at the planning
and construction phase, all remains finely balanced on loose rubble.
Encouraged at every turn to "think outside the box", perhaps it's time for a closer look
at what got us into boxes in the first place. This presentation will reveal the original
ratios and exact dimensions of the upper and middle chambers labelled "kings"
and "queens", centuries ago, by people who didn't know why.
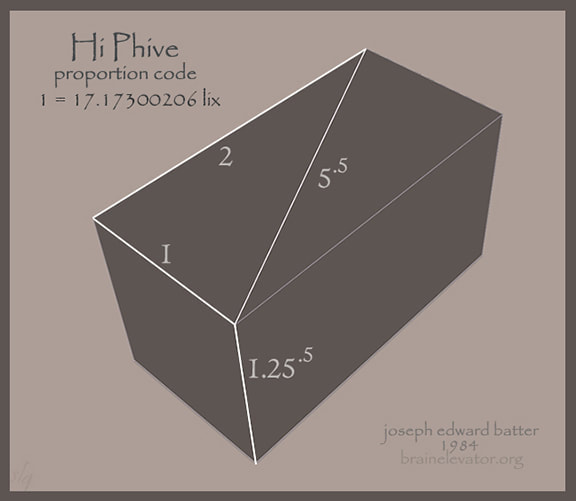
From here on in, they are designated "Hi Phive" and "Point Phive", respectively
for reasons that will become obvious within a few minutes.
As you proceed, keep in mind. Ahead are precise scale models of existing structures
designed and assembled in prehistory, before the catastrophe that drove
humanity mad by amnesia fell upon us.
Cross section ( detail ), of the Great Pyramid at Gizeh,
Number 5 on the lix grid.
Number 5 on the lix grid.
phive
to the power of point phive
times point phive
plus point phive
equals phi
to the power of point phive
times point phive
plus point phive
equals phi
The "lix", unit is base 10, and ever so slightly longer than a foot.
Been around longer too. That little difference is a big deal.
1 lix = 1.001006(153) feet
"Pyramidologists have long known the Gizeh pyramids were not designed with the base 12,
British inch, that the "primitive inch", was slightly longer. Piazzi-Smyth, in the mid-nineteenth
century determined the conversion to be approximately 1.001.
Dr Adam Rutherford, (1957), using more modern instruments, placed it at 1.00106 .
"Rutherford brought the most advanced equipment and professional surveyors to measure
and decode the Great Pyramid. Despite his unwavering belief in a biblical source for the
design of the structure, (and any measurement beyond 5 decimals was superfluous), a
sincere effort was applied to produce a cross-section with a coherent trigonometric
application of the measurements. Rutherford and his team produced
the most reliable dimensions to date". (j.e.b. 1986)
The Pyramid was measured in British inches then converted, divided by 1.00106, into
primitive inches. Rutherford settled on the height of the so called "king's", chamber
at 230.38871 primitive inches, or, divide by 12, = 19.199059 primitive feet.
Had he rounded the height to 19.2, all you will learn here,
and so much more, would have become instantly transparent.
The key to decoding was to convert Rutherford's base 12, 'primitive inch',
measurements into base 10 lix, then relate the chamber dimensions to one another.
We didn't need to round it off:
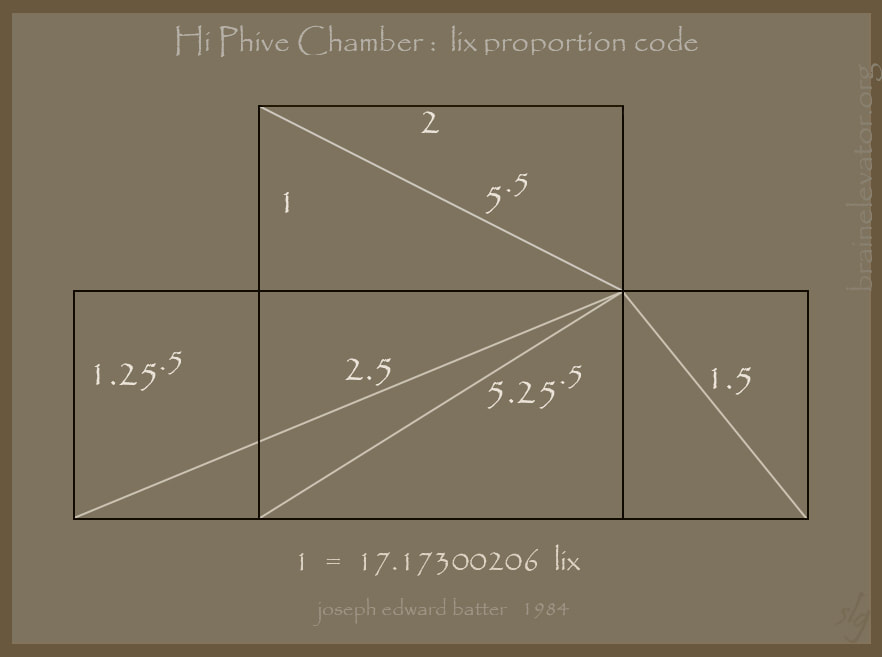
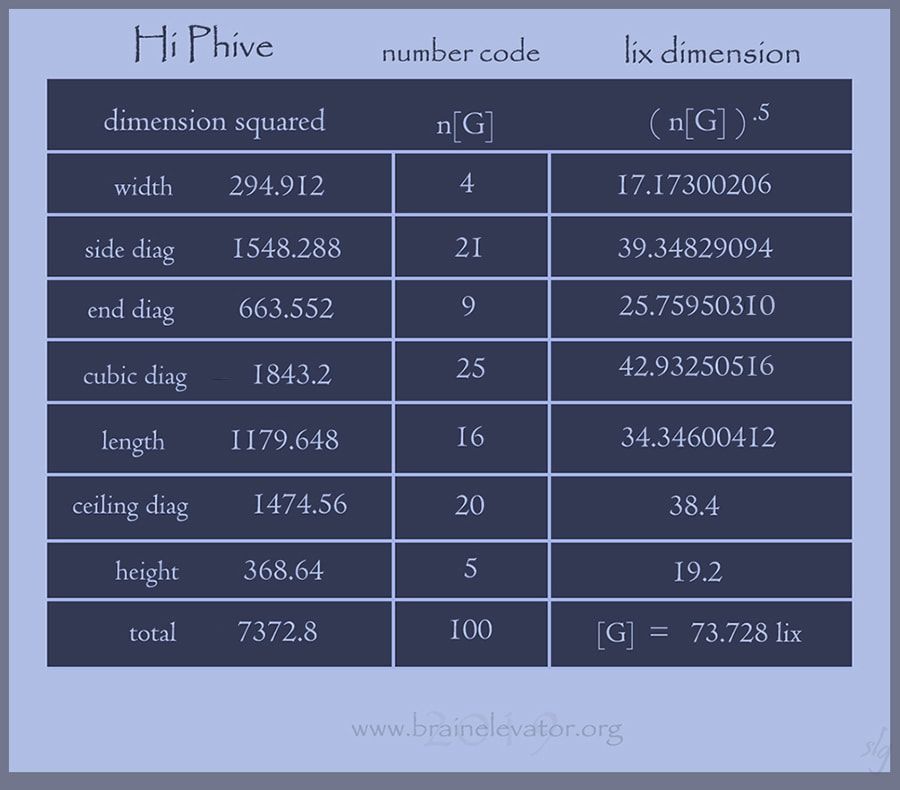
19.2 lix, ( 2 to the 6th x .3 ), is the height of the chamber.
Divided by the square root of 1.25, ( phi - .5 ), equals the width:
17.17300206 lix
The width is half the length and the height is half the diagonal.
"Pyramidologists have long known the Gizeh pyramids were not designed with the base 12,
British inch, that the "primitive inch", was slightly longer. Piazzi-Smyth, in the mid-nineteenth
century determined the conversion to be approximately 1.001.
Dr Adam Rutherford, (1957), using more modern instruments, placed it at 1.00106 .
"Rutherford brought the most advanced equipment and professional surveyors to measure
and decode the Great Pyramid. Despite his unwavering belief in a biblical source for the
design of the structure, (and any measurement beyond 5 decimals was superfluous), a
sincere effort was applied to produce a cross-section with a coherent trigonometric
application of the measurements. Rutherford and his team produced
the most reliable dimensions to date". (j.e.b. 1986)
The Pyramid was measured in British inches then converted, divided by 1.00106, into
primitive inches. Rutherford settled on the height of the so called "king's", chamber
at 230.38871 primitive inches, or, divide by 12, = 19.199059 primitive feet.
Had he rounded the height to 19.2, all you will learn here,
and so much more, would have become instantly transparent.
The key to decoding was to convert Rutherford's base 12, 'primitive inch',
measurements into base 10 lix, then relate the chamber dimensions to one another.
We didn't need to round it off:
19.2 lix, ( 2 to the 6th x .3 ), is the height of the chamber.
Divided by the square root of 1.25, ( phi - .5 ), equals the width:
17.17300206 lix
The width is half the length and the height is half the diagonal.
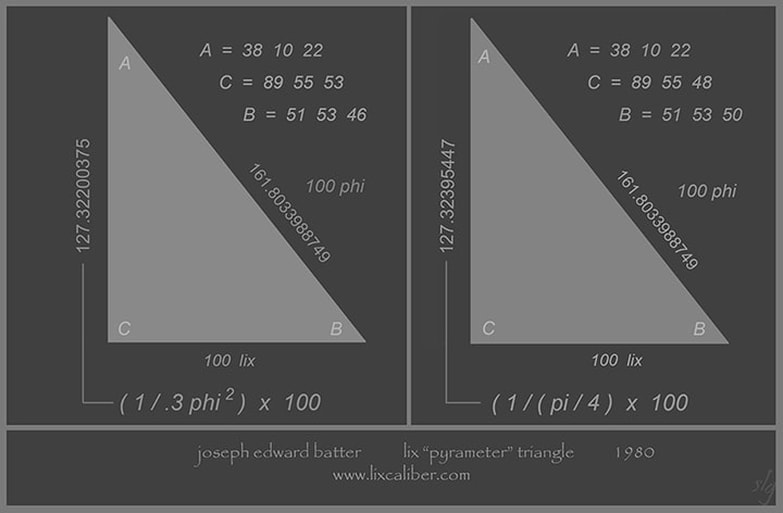
In 1980, design draughtsman, Joseph Edward Batter and i located the "lix", unit,
by way of the astronomical unit, light speed, pi and the Golden ratio.
When he established the "lix grid", with the "pyrameter triangle(s)", and plotted a 1/200
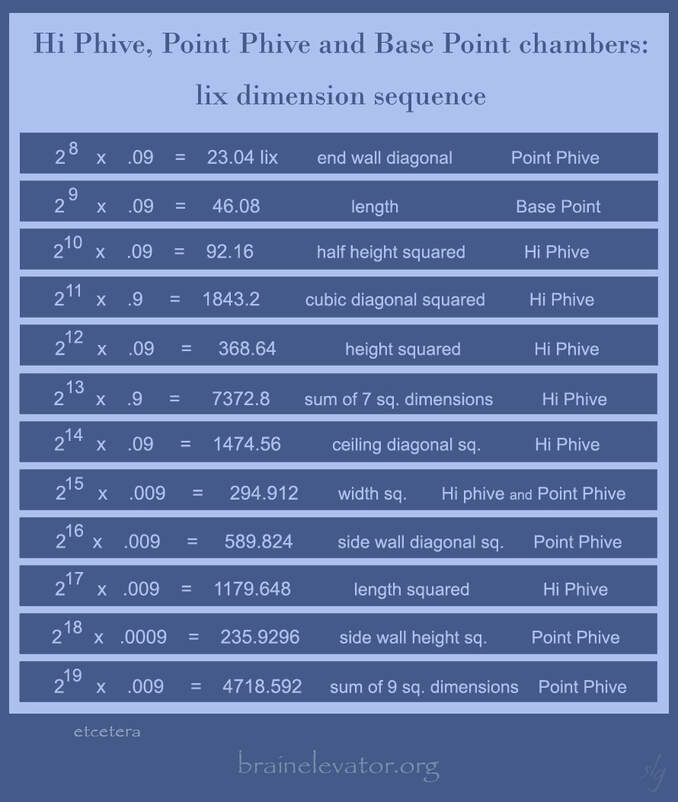
cross-section of the Great Pyramid on it, four "Hi Phive", chamber codes were revealed.
cross-section of the Great Pyramid on it, four "Hi Phive", chamber codes were revealed.
They are a Song of Joy to Number. At the very foundations of "Earth Measure".
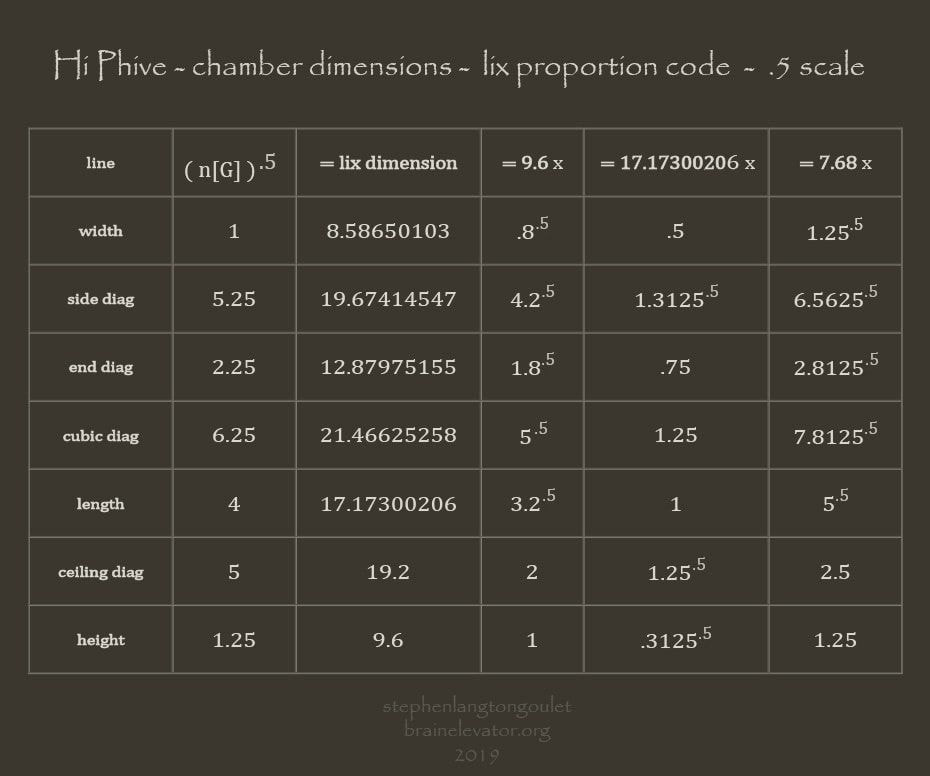
Here is your opportunity to reveal the "as built", dimensions of the most
well known and least understood rectangular cube in recorded history.
With a notepad, pen and calculator, enter 17.17300206, the width,
into memory and multiply it by each of the other six factors:
well known and least understood rectangular cube in recorded history.
With a notepad, pen and calculator, enter 17.17300206, the width,
into memory and multiply it by each of the other six factors:
.....now, square each one.....then add them up.....
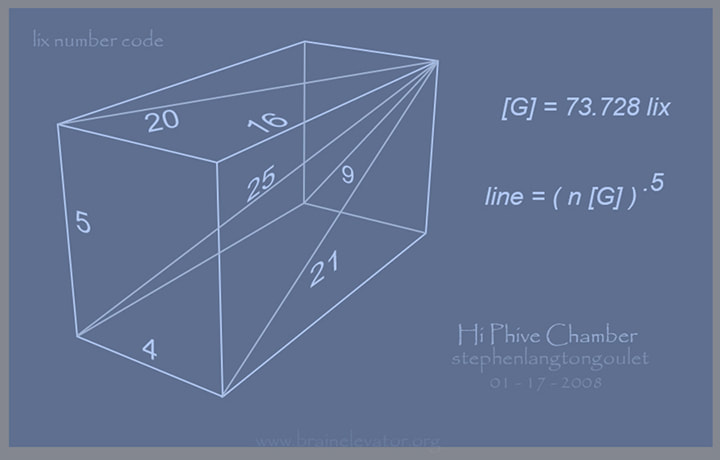
In 2008, i found a 5th code and a remarkable module, 73.728 lix. It led to "Point Phive",
(queen's) chamber geometry, Simpson's primitive inch "unit dimension", code and
a wondrous artifact i had no choice but to call a "brainelevator".
the Numerical Source of Great Pyramid Chamber Dimensions
In 2008, i found a 5th code and a remarkable module, 73.728 lix. It led to "Point Phive",
(queen's) chamber geometry, Simpson's primitive inch "unit dimension", code and
a wondrous artifact i had no choice but to call a "brainelevator".
the Numerical Source of Great Pyramid Chamber Dimensions
4 21 9 25 16 20 5
Square Root Cellar?
The choice of monetary units also reflect hints of the original number and measurement system:
0 - 1 - 2 - 5
0 - 1 - 2 - 5
I often pause here. A favorite bench, with an astonishing view:
103.03801240, squared = 10616.832 = 144 x 73.728
Circling the Squaring
April 10 2020
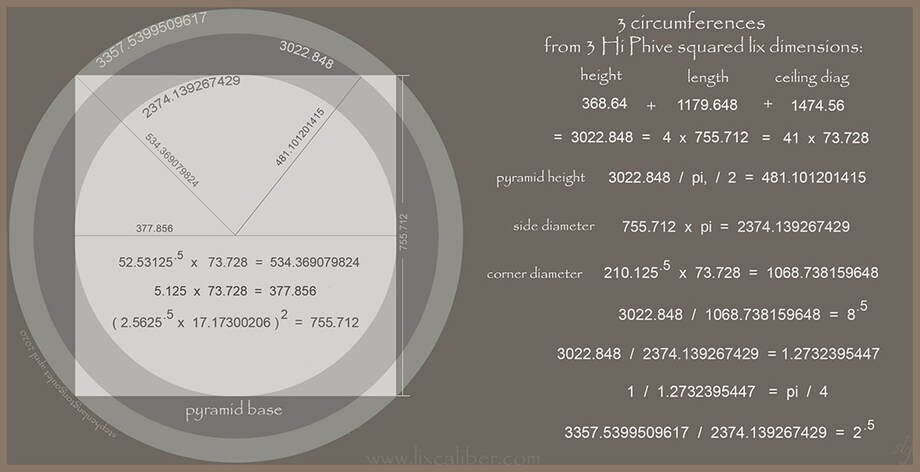
At this point let's step outside for a brief thousand pace walk around
the Pyramid base, bringing along the height, length and ceiling diagonal,
squared dimensions, from Hi Phive to guide us.
Every square describes three circles. The inner one touches the sides, the outer,
the corners. The ratio between these two is the square root of 2.
The third circumference, in between the two, is the sum of the four sides of the square.
The ratio between it and the diameter of the outer circle
is the square root of 8.
April 10 2020
At this point let's step outside for a brief thousand pace walk around
the Pyramid base, bringing along the height, length and ceiling diagonal,
squared dimensions, from Hi Phive to guide us.
Every square describes three circles. The inner one touches the sides, the outer,
the corners. The ratio between these two is the square root of 2.
The third circumference, in between the two, is the sum of the four sides of the square.
The ratio between it and the diameter of the outer circle
is the square root of 8.
Yes, we just pulled the base and height of the Great Pyramid
from three squared dimensions of the Hi Phive chamber!
Base perimeter as a circumference of 3022.848, divided by pi,
diameter: 962.202402830, / 2 = radius: 481.101201415 lix
2 to the 13th, x .369 = 3022.848
3022.848 / 4 = 10.25 x 73.728 = 755.712 = side length
755.712 - 737.28 = 18.432, x 100 = Hi Phive, cubic diagonal squared
Which brings us neatly back inside
for your introduction to the middle chamber:
June 15, 2008
No monarch was ever interred in the "queens", chamber, either. As with the upper chamber,
designation should reflect the purpose within the design and is hereafter referred to
as the "Point Phive", chamber.
With 73.728 resolved it seemed likely the module could be applied to other areas of the Pyramid.
I knew the width of the middle chamber was exactly the same as Hi Phive, 17.17300206 lix,
but had no idea what the other dimensions were.
I was surprised to find William Kelly Simpson had already deduced part of the “kings”, chamber
number sequence using a unit dimension of 103.03, primitive inches, half the width.
chamber width: 206.06, / 12 = 17.17166666..., primitive feet
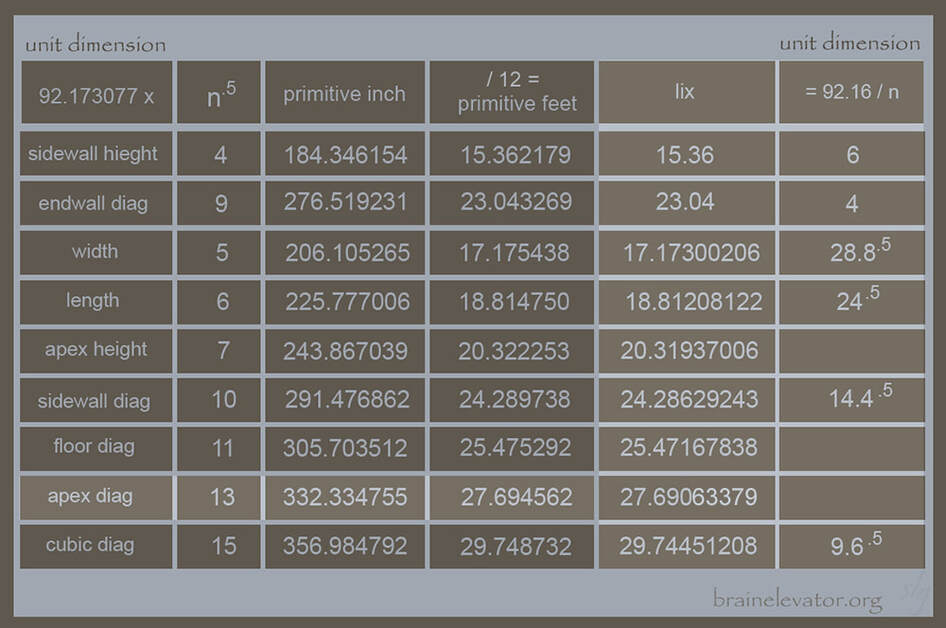
More interesting for me was his discovery of a middle chamber number sequence.
Simpson deduced numerical relationships in the chamber applying a “unit dimension”,
of 92.173077, primitive inches, half the side wall height, and the square roots of:
4, 5, 6, 7, 9, 10, 11 and 15.
(This series is missing a few dimensions, such as 13, the apex diagonal. On his published chart:
the side wall diagonal, 10, and the floor diagonal, 11, are switched. Corrected below.)
Simpsons “queen’s”, chamber width:
92.173077 x sq-rt 5 = 206.105265 primitive inches, / 12
= 17.175438 primitive feet.
As you will see, had Simpson employed a unit dimension of 92.16, (9.6 sq.)
the original design specifications for the middle chamber of the Great Pyramid
would have instantly revealed themselves.
92.16 x 1.25 to the power of .5 = 103.03801240, Hi Phive perimeter
92.16 divided by 1.25 = 73.728
92.173077 x sq-rt 5 = 206.105265 primitive inches, / 12
= 17.175438 primitive feet.
As you will see, had Simpson employed a unit dimension of 92.16, (9.6 sq.)
the original design specifications for the middle chamber of the Great Pyramid
would have instantly revealed themselves.
92.16 x 1.25 to the power of .5 = 103.03801240, Hi Phive perimeter
92.16 divided by 1.25 = 73.728
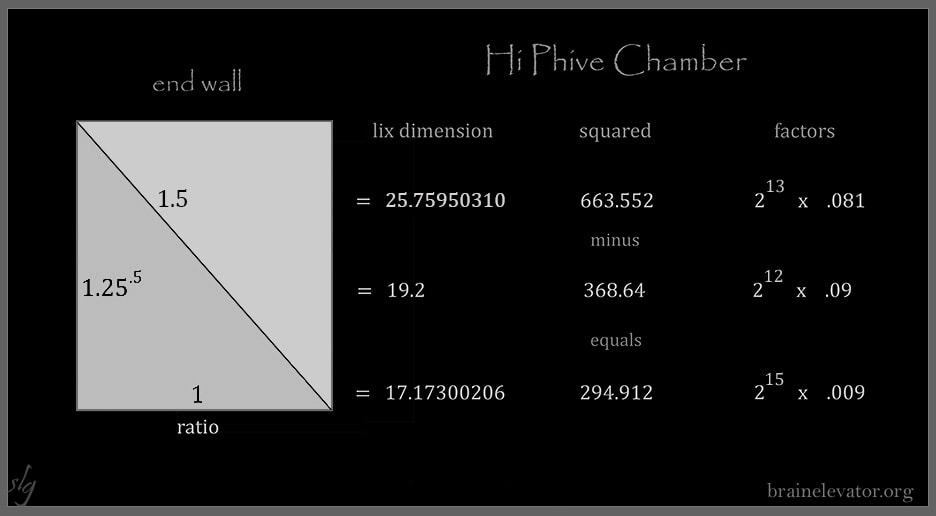
In the last column, 7, 11, 13, are blank. They found another way in,
by way of the lix factor code, (revealed below).
The side wall height, 15.36, plus the end wall diagonal, 23.04,
equals 38.4, the ceiling diagonal of Hi Phive.
Knowing the width of both chambers are equal i divided it by the square root of 5
and found Simpsons', unit dimension, half the sidewall height, is exactly 7.68 lix.
primitive inches 92.173077, / 12 = 7.681089 primitive feet
17.17300206 / 2.2360679775 = 7.68000000125 lix
7.68 = 2 to the 8th, x .03
In the Hi Phive chamber: 17.17300206 x 2.2360679775 = 38.4 lix, the ceiling diagonal.
In the Point Phive chamber: 17.17300206 / 2.2360679775 = 7.68 lix, half the side wall height.
chamber width = 7.68 x 2.2360679775 = 17.17300206 lix, squared = 294.912
7.68 squared x 10 = 589.824 = side wall diagonal squared = 294.912 x 2
The sidewall height of the Point Phive chamber: 15.36 lix
multiplied by the height of the Hi Phive chamber: 19.2 lix
= 294.912, their common width:
17.17300206 lix, squared.
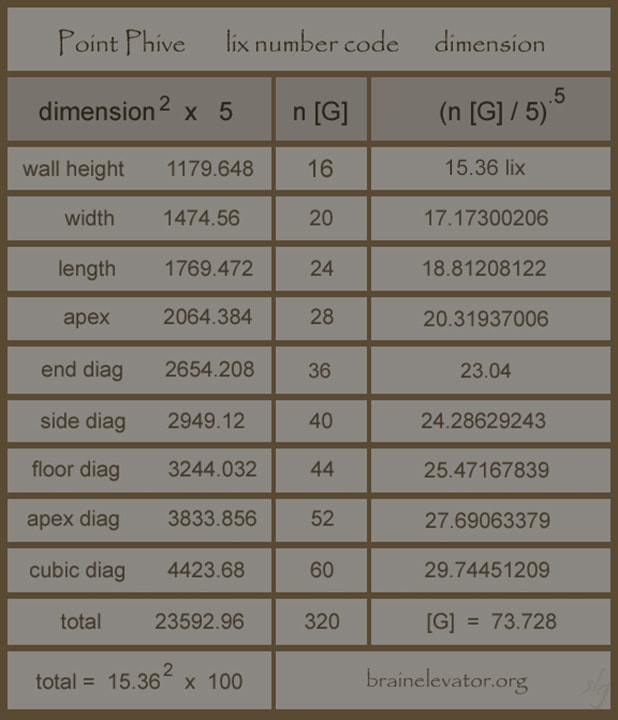
lix number code
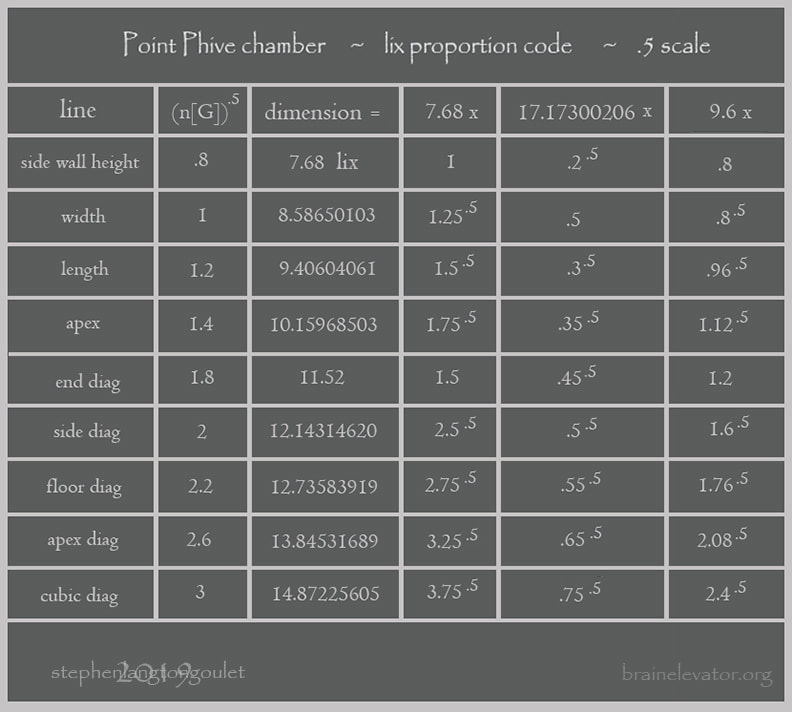
At actual size, "Point Phive", chamber dimensions are also revealed
through the lix number code, with one extra step:
by way of the lix factor code, (revealed below).
The side wall height, 15.36, plus the end wall diagonal, 23.04,
equals 38.4, the ceiling diagonal of Hi Phive.
Knowing the width of both chambers are equal i divided it by the square root of 5
and found Simpsons', unit dimension, half the sidewall height, is exactly 7.68 lix.
primitive inches 92.173077, / 12 = 7.681089 primitive feet
17.17300206 / 2.2360679775 = 7.68000000125 lix
7.68 = 2 to the 8th, x .03
In the Hi Phive chamber: 17.17300206 x 2.2360679775 = 38.4 lix, the ceiling diagonal.
In the Point Phive chamber: 17.17300206 / 2.2360679775 = 7.68 lix, half the side wall height.
chamber width = 7.68 x 2.2360679775 = 17.17300206 lix, squared = 294.912
7.68 squared x 10 = 589.824 = side wall diagonal squared = 294.912 x 2
The sidewall height of the Point Phive chamber: 15.36 lix
multiplied by the height of the Hi Phive chamber: 19.2 lix
= 294.912, their common width:
17.17300206 lix, squared.
lix number code
At actual size, "Point Phive", chamber dimensions are also revealed
through the lix number code, with one extra step:
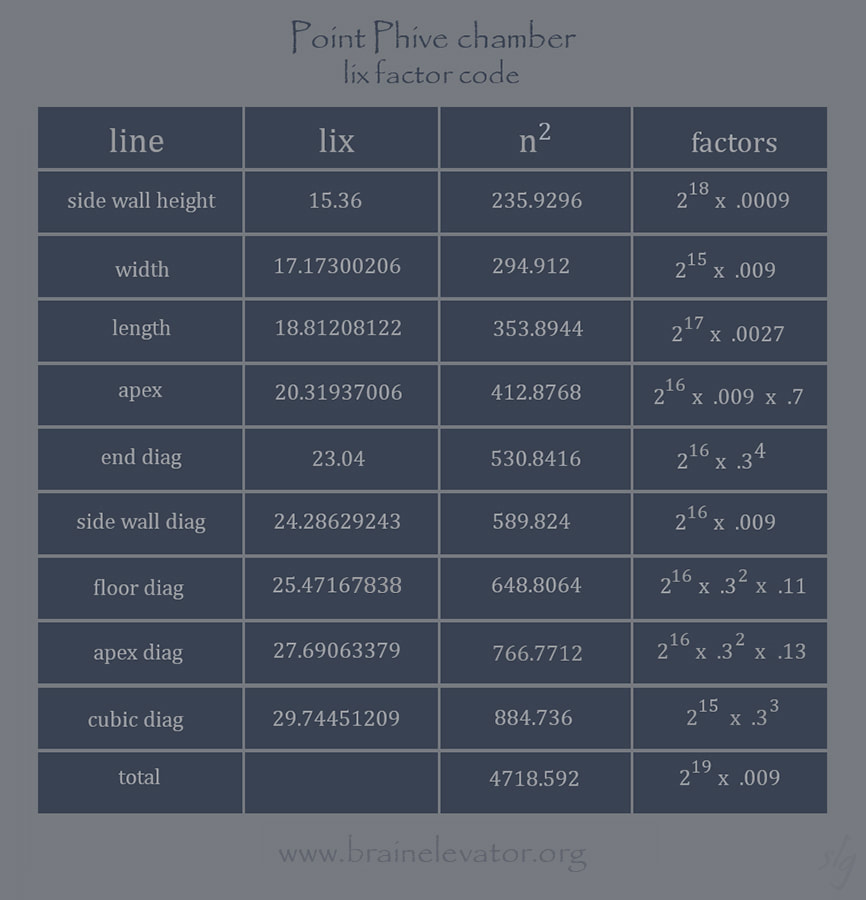
square root cellar, too:
.7, .11, .13
without them, the entire construct collapses.
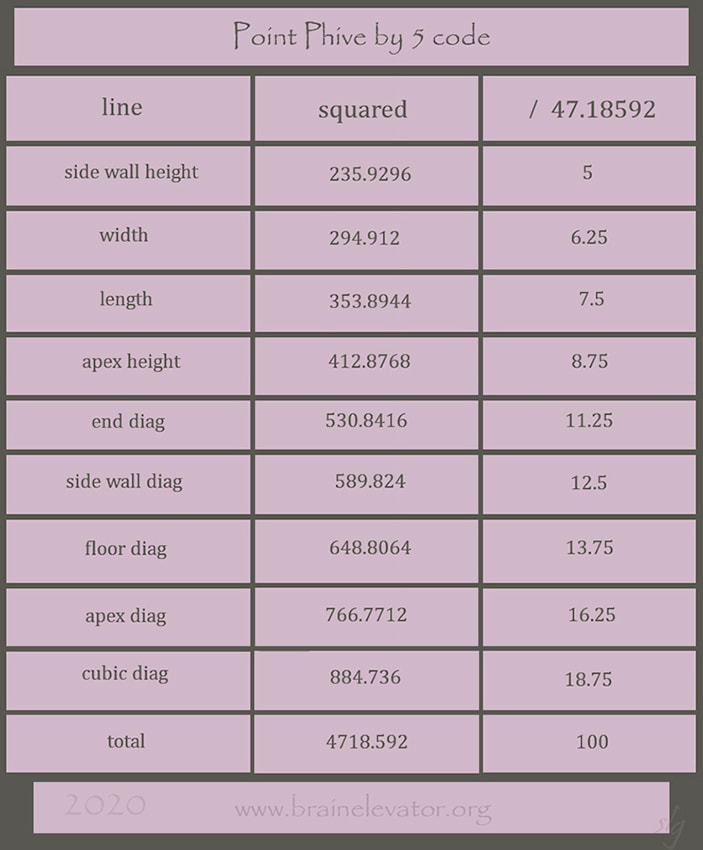
The sum of the 9 squared dimensions: 4718.592 = 4 cubed x 73.728
Remembering, the sum of Hi Phive's 7 squared dimensions = 7372.8
7372.8 / 4718.592 = 1.5625 = 1.25 sq.
Three squared dimensions: height, length and ceiling diagonal of the Hi Phive chamber
add up to the actual pyramid base: 368.64 + 1179.648 + 1474.56 = 3022.848 lix.
16 squared dimensions of both chambers add up to a pyramid base
four times larger: 7372.8 + 4718.592 = 12091.392, divided by 4 = 3022.848
As a circumference: 12091.392
divided by pi = 3,848.809611323, diameter
divided by 2 = 1,924.404805661, radius
equals the as built pyramid height:
481.101201415 lix, x 4
It would be difficult to conceal such a wonder.
12091.392 - 10616.832, (Hi Phive perimeter squared),
= 1474.56, Hi Phive ceiling diagonal, squared.
both chambers, width = 17.17300206,
x 4 = 68.69200824, squared = 4718.592
reminder..... Hi Phive "number", code: 4, 21, 9, 25, 16, 20, 5, adds up to 100 as well.
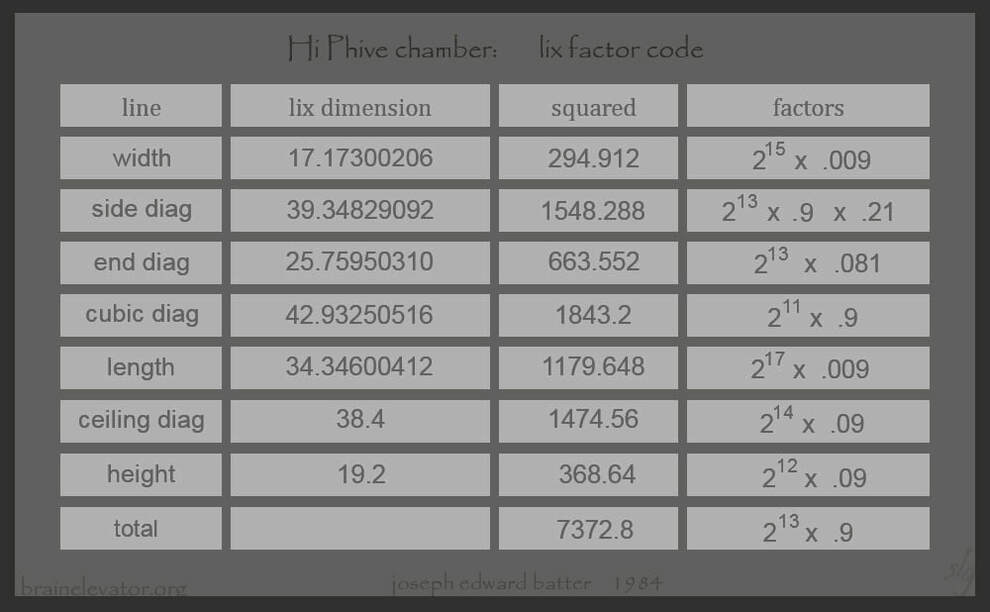
lix factor code, recap:
Newly discovered "Base Point", (subterranean), chamber dimensions
are revealed near the end of this presentation.
lix factor code, recap:
Newly discovered "Base Point", (subterranean), chamber dimensions
are revealed near the end of this presentation.
Hi Phive floor, area: 17.17300206 x 34.34600412 = 589.824
= side wall diagonal squared, Point Phive.
Point Phive: floor dimensions, based on a, "unit dimension",
of half the sidewall height: 15.36 / 2 = 7.68 lix
= side wall diagonal squared, Point Phive.
Point Phive: floor dimensions, based on a, "unit dimension",
of half the sidewall height: 15.36 / 2 = 7.68 lix
area of the floor: 17.17300206 x 18.81208122 = 323.05991
= the square root of 19.2, x 73.728
= the square root of 19.2, x 73.728
"Degrees of Certainty"
06 - 18 - 2020
This day, a startling series of ratios materialized out of my, "Indig Square of Nines",
recently posted to sister site, lixcaliber.com. What follows is a clear and concise iteration
of modules, ratios and chamber dimensions, apparently, from outside the chambers,
beyond the pyramid itself.
Imagine my astonishment:
180 / 1.25 to the 4th power = 73.728
180 / 1.25 to the 4th power = 73.728
Remarkable affirmations, taking us back to the beginning, to 1.25, introducing
7.68 and 9.6, half the chamber heights, all the while circling the entrance
to the brainelevator with a sublime flourish i never imagined possible,
or even necessary, a few days prior.
7.68 and 9.6, half the chamber heights, all the while circling the entrance
to the brainelevator with a sublime flourish i never imagined possible,
or even necessary, a few days prior.
excerpt, "Knowledge of the Forever Time"
"The mathematician sees the wonder of the Great Pyramid of Egypt and with mathematics he sets out
to reveal the purpose of its creation. He will count the stones, measure the heights, weigh, divide, calculate
and subtract. He will obtain the mean, the angle, the footage, the pi and the circumference, and, when he is
finished, he will walk away bewildered and scratching his head. He will leave it no more certain
than he did when he came to it." Damon T Berry
or not.....
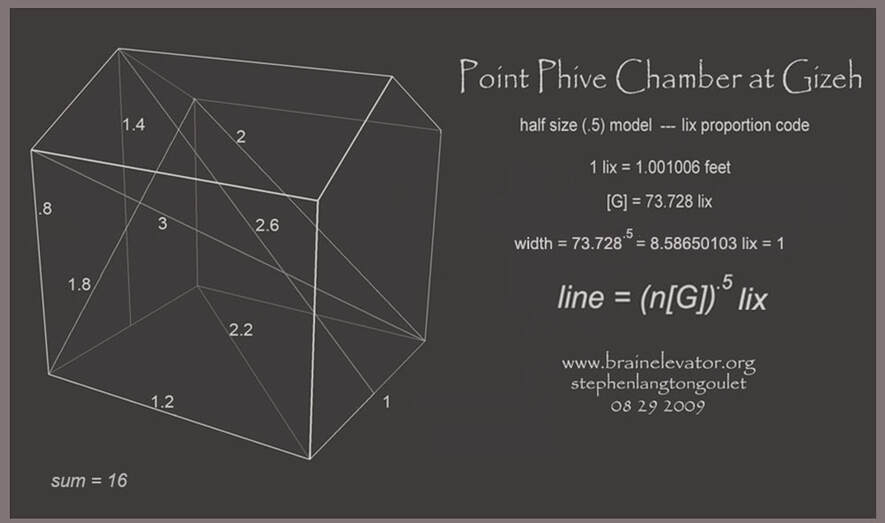
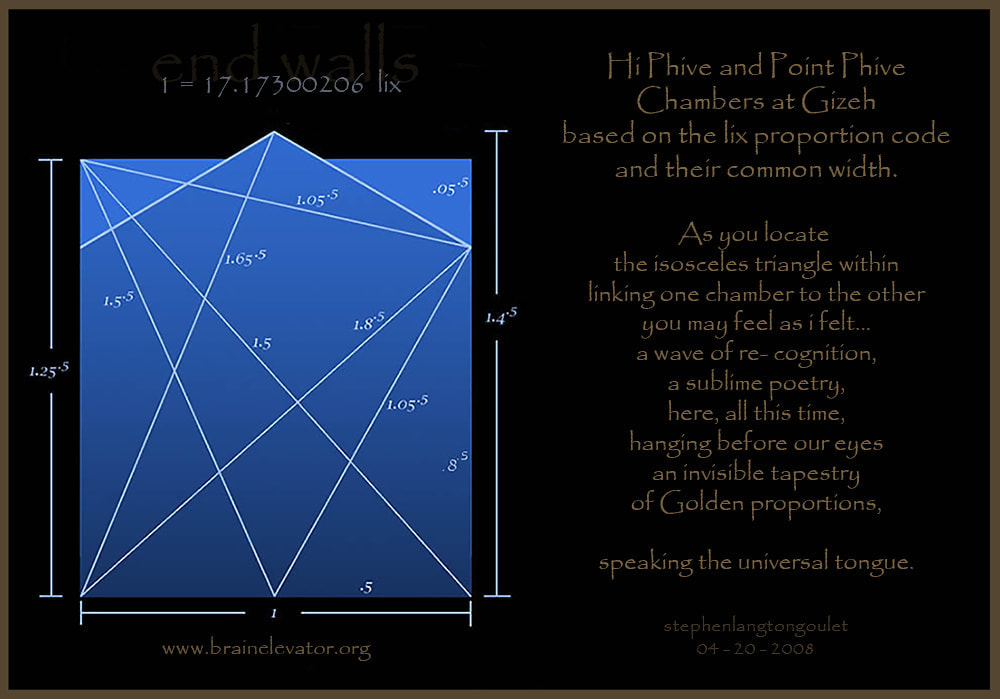
Realizing how the two upper chambers of the Great Pyramid at Gizeh fit geometrically
inside each other, i imagined the next logical step was build a model. It was fortuitous
when economic factors determined the prototype would be half size, because here
the lix dimension formulas are revealed at their most eloquent,
beginning with a profound reciprocity.....
"The mathematician sees the wonder of the Great Pyramid of Egypt and with mathematics he sets out
to reveal the purpose of its creation. He will count the stones, measure the heights, weigh, divide, calculate
and subtract. He will obtain the mean, the angle, the footage, the pi and the circumference, and, when he is
finished, he will walk away bewildered and scratching his head. He will leave it no more certain
than he did when he came to it." Damon T Berry
or not.....
Realizing how the two upper chambers of the Great Pyramid at Gizeh fit geometrically
inside each other, i imagined the next logical step was build a model. It was fortuitous
when economic factors determined the prototype would be half size, because here
the lix dimension formulas are revealed at their most eloquent,
beginning with a profound reciprocity.....
Every 1 x 2 rectangle in the known Universe contains:
the height of the Hi Phive chamber
(half the diagonal: 1.25 to the power of .5)
every other dimension within it
every dimension of the Point Phive chamber below it
the entire structure around it
and ultimately back
to where we found the lix unit
in planetary geometric centers arrayed
on an expanding golden ratio grid.
That's some rectangle.
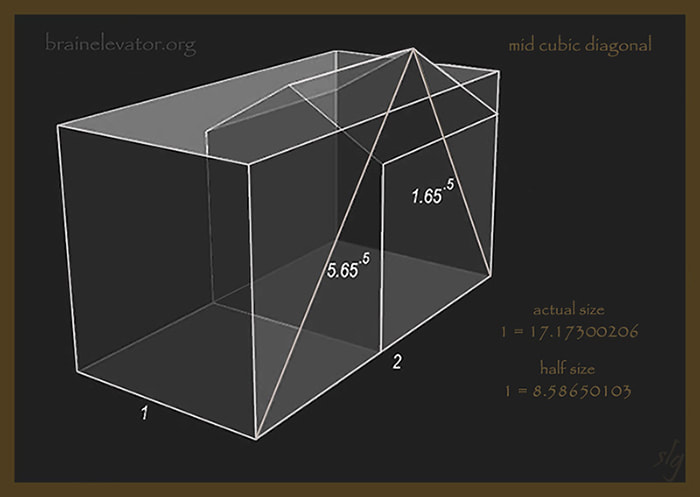
The volume of every rectangular cube with these proportions:
1 x 2 x 1.1180339887..... = 5 to the power of .5
Some things are beyond the capacity of metaphor to convey
and one simply has to take some time and do the math.
brainelevator: first
and one simply has to take some time and do the math.
brainelevator: first
The volume at this scale is 1415.5776 cubic lix = 19.2 x 73.728
In the Point Phive chamber, the floor diagonal, squared: 648.8064
plus the apex diagonal, squared, 766.7712, = 1415.5776,
and, the cubic diagonal, squared, 884.736, plus
the end wall diagonal, squared, 530.8416 = 1415.5776
The actual length of Point Phive = 18.81208122 lix,
x 2 = 37.62416244, squared, = 1415.5776
brainelevator: second
The claim, for generations, that nothing is perfect, always made
me wonder what we keep such a perfect word around for.
In the Point Phive chamber, the floor diagonal, squared: 648.8064
plus the apex diagonal, squared, 766.7712, = 1415.5776,
and, the cubic diagonal, squared, 884.736, plus
the end wall diagonal, squared, 530.8416 = 1415.5776
The actual length of Point Phive = 18.81208122 lix,
x 2 = 37.62416244, squared, = 1415.5776
brainelevator: second
The claim, for generations, that nothing is perfect, always made
me wonder what we keep such a perfect word around for.
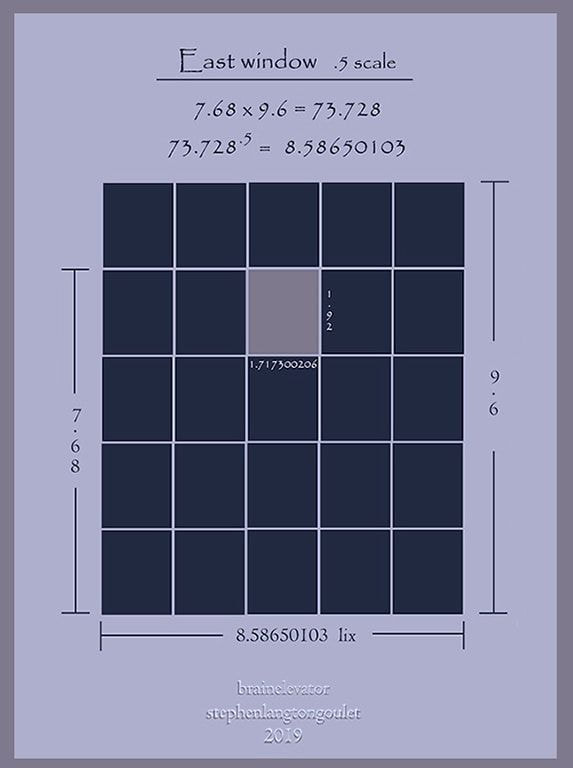
25 / 16 = 1.5625 = 1.25 sq.
On the half size model
centered and 1/5 down from the top
a 1/25 sized window is placed.
Height is 1/10 the ceiling diagonal: 1.92
Width is 1/10 the length: 1.717300206
250 of these, "windows", or mirrors, will completely cover the interior of Hi Phive.
West end walls overlaid, actual size:
West end walls overlaid, actual size:
"3Ten (triten) Measure, the Legend of Joey Bee", plots planetary mean distances
on an expanding golden ratio grid, with "lixcaliber", the Mother of all Scales,
found embedded, now emerging, from the heart of the Great Pyramid,
through slope angle, number 5.
1 : 200, cross section of the Great Pyramid, based on the "pyrameter", triangle.
For now, "The Machine Array", speaks for itself.
Four scale drawings comprise the series. The other two,
"Venus (mind/heart)", and "The S.E.A. of the Machine Array",
await in the wings.
exterior dimensions
phi to the 16th, by phi to the 17th power, divided by 1000
2.207 x 3.571 lix
phi = 1.6180339887....
n phibonacci x 5 to the power of .5 = n lucas
ex: 19 phibo = 4181, x 2.2360679775 = 9349 = 19 lucas
phi to the 19th = 9349.000101
A few years back a lidar image of the Great Pyramid was released revealing a cloudy cigar
shape above the Grande Gallery. On both of the drawings above, a twisting series of 6
squares emerges from the line of Venus ( 2 ) where 13 lines meet, suggesting
a chamber running 90 degrees, east/west, from the others.
A 45 degree angle through the largest square touches, "10", one lix, on lixcaliber.
The "Mother of all Scales", the first artifact Joe and i found within the Pyramid,
was located at this position after nearly all the other lines were rendered.
Four scale drawings comprise the series. The other two,
"Venus (mind/heart)", and "The S.E.A. of the Machine Array",
await in the wings.
exterior dimensions
phi to the 16th, by phi to the 17th power, divided by 1000
2.207 x 3.571 lix
phi = 1.6180339887....
n phibonacci x 5 to the power of .5 = n lucas
ex: 19 phibo = 4181, x 2.2360679775 = 9349 = 19 lucas
phi to the 19th = 9349.000101
A few years back a lidar image of the Great Pyramid was released revealing a cloudy cigar
shape above the Grande Gallery. On both of the drawings above, a twisting series of 6
squares emerges from the line of Venus ( 2 ) where 13 lines meet, suggesting
a chamber running 90 degrees, east/west, from the others.
A 45 degree angle through the largest square touches, "10", one lix, on lixcaliber.
The "Mother of all Scales", the first artifact Joe and i found within the Pyramid,
was located at this position after nearly all the other lines were rendered.
"......that they will know we were here....."
Consider, at a particular point in the distant past, a desperate need to preserve
critical information arises. The severity of the crisis suggests dozens or even
hundreds of generations may pass before the information will be
rediscovered, let alone translated and understood.
Looking back, at the certainty of doom those people faced, one can't help but marvel
at the courage, dedication and sacrifice, en masse, to expend their final generations
preserving all they valued most, for an unknown and uncertain future people.
It staggers the mind, that level of commitment.
Additionally, how could a valuable trove of essential knowledge be kept safe,
and unblemished, when even the most robustly constructed "libraries",
eventually crumble, submerge or burn?
Their plan was the Great Pyramid.
The system of Measure guiding their purpose
lays out the foundation of their message.
Its language is universal:
1 / phi = phi - 1 phi squared = phi + 1
.61803398874989 x .61803398874989 + .61803398874989 = 0.999999999999989
Locating the "lix unit", in the planetary mean distances and the scale "lixcaliber",
in the heart of the Great Pyramid was, and remains, a transcendent experience.
Years later, witnessing a "brainelevator", emerge from the combined chamber
dimensions, as a crystal unfolding in the air around me, ever more so.
That said, no "speculations" are made here about the source of this geometry, beyond the obvious:
It had to be well known long before a "lix", pyramid at Gizeh could be designed and assembled.
Furthermore, any opinions i might opine on, as an artist, would be woefully inadequate
as i am, by no measure, a mathematician, archaeologist, engineer, pyramidologist,
cosmologist, or prehistorian to offer such context.
The irony, that once this information is well understood, it will likely shake those professions
as well as many others, to their foundations, is not lost on me. Clearly, this will be part
of a larger discussion i look forward to participating in.
In the face of resplendent measurement codes and ratios, extensive reflection
will achieve far greater insights than intensive conjecture ever has.
Joe and i pried a few cold stones aside, far enough to let some light inside.
After four decades within this work, light continues pouring out.
There is one thing i recognized early. "Civilization", got off on the wrong Foot.
pass it on
We put too much into this work to waste your time so if you made it through intact, albeit a
few white hairs, know, i admire and appreciate your patience and attention to detail. Should
you recognize something here, beyond metaphor's capacity to explain away, dig in and learn
the ratios, modules and dimensions. Go where the numbers lead. Confirm, connect and verify
each step. And, when you remember how you arrived there, let us know where it fits.
I continue to believe, recent developments notwithstanding,
we've barely scratched the surface. For instance:
Consider, at a particular point in the distant past, a desperate need to preserve
critical information arises. The severity of the crisis suggests dozens or even
hundreds of generations may pass before the information will be
rediscovered, let alone translated and understood.
Looking back, at the certainty of doom those people faced, one can't help but marvel
at the courage, dedication and sacrifice, en masse, to expend their final generations
preserving all they valued most, for an unknown and uncertain future people.
It staggers the mind, that level of commitment.
Additionally, how could a valuable trove of essential knowledge be kept safe,
and unblemished, when even the most robustly constructed "libraries",
eventually crumble, submerge or burn?
Their plan was the Great Pyramid.
The system of Measure guiding their purpose
lays out the foundation of their message.
Its language is universal:
1 / phi = phi - 1 phi squared = phi + 1
.61803398874989 x .61803398874989 + .61803398874989 = 0.999999999999989
Locating the "lix unit", in the planetary mean distances and the scale "lixcaliber",
in the heart of the Great Pyramid was, and remains, a transcendent experience.
Years later, witnessing a "brainelevator", emerge from the combined chamber
dimensions, as a crystal unfolding in the air around me, ever more so.
That said, no "speculations" are made here about the source of this geometry, beyond the obvious:
It had to be well known long before a "lix", pyramid at Gizeh could be designed and assembled.
Furthermore, any opinions i might opine on, as an artist, would be woefully inadequate
as i am, by no measure, a mathematician, archaeologist, engineer, pyramidologist,
cosmologist, or prehistorian to offer such context.
The irony, that once this information is well understood, it will likely shake those professions
as well as many others, to their foundations, is not lost on me. Clearly, this will be part
of a larger discussion i look forward to participating in.
In the face of resplendent measurement codes and ratios, extensive reflection
will achieve far greater insights than intensive conjecture ever has.
Joe and i pried a few cold stones aside, far enough to let some light inside.
After four decades within this work, light continues pouring out.
There is one thing i recognized early. "Civilization", got off on the wrong Foot.
pass it on
We put too much into this work to waste your time so if you made it through intact, albeit a
few white hairs, know, i admire and appreciate your patience and attention to detail. Should
you recognize something here, beyond metaphor's capacity to explain away, dig in and learn
the ratios, modules and dimensions. Go where the numbers lead. Confirm, connect and verify
each step. And, when you remember how you arrived there, let us know where it fits.
I continue to believe, recent developments notwithstanding,
we've barely scratched the surface. For instance:
January 5, 2023
The point where the center line of the pyramid
touches the base of the subterranean chamber.
The point where the center line of the pyramid
touches the base of the subterranean chamber.
After several frustrated attempts over the years, a door finally
opened into, "subterranean" , chamber geometry. At least part way:
opened into, "subterranean" , chamber geometry. At least part way:
ratio: 46.08 divided by 26.83281574 = 1.717300206 lix
46.08 lix is twice the end wall diagonal of the Point Phive chamber, 23.04.
The width of Hi Phive and Point Phive: 17.17300206, here, 1/10th smaller,
and it's square, 294.912, 1/100th smaller.
281.25 appears in the half size dimensions of the Hi Phive chamber
as a factor of the length of the end wall diagonal:
the square root of 2.8125, x 7.68.
and 720?
time will tell
and time told.....April, 2024:
3 divided by 1.25 = 2.4
2.4 divided by 1.25 = 1.92
1.92 divided by 1.25 = 1.536
46.08 lix is twice the end wall diagonal of the Point Phive chamber, 23.04.
The width of Hi Phive and Point Phive: 17.17300206, here, 1/10th smaller,
and it's square, 294.912, 1/100th smaller.
281.25 appears in the half size dimensions of the Hi Phive chamber
as a factor of the length of the end wall diagonal:
the square root of 2.8125, x 7.68.
and 720?
time will tell
and time told.....April, 2024:
3 divided by 1.25 = 2.4
2.4 divided by 1.25 = 1.92
1.92 divided by 1.25 = 1.536
720 divided by 1.25 = 576 = 192 x 3
576 divided by 1.25 = 460.8 = length, Base Point chamber, x 10
460.8 divided by 1.25 = 368.64 = 19.2, squared
368.64 divided by 1.25 = 294.912 = 17.17300206, squared
294.912 divided by 1.25 = 235.9296 = 15.36 squared
15.36 x 19.2 = 294.912, width: 17.17300206, squared, both chambers
"dystillations"
A final graphic for those who jumped to the end for the expected gist, soundbite,
hashtag, meme or punchline; without doing the math and proofing it yourself:
#twochamberscomposedofeachother
hashtag, meme or punchline; without doing the math and proofing it yourself:
#twochamberscomposedofeachother
An introduction to the "lix coffer code", and it's relation to
the planetary geometric centres, on the lix grid, will be posted next.
Seeking can become a lifelong passion.
Finding presents a fundamentally different challenge.
As it turns out, by any metric, having to re-ruler the World alone, is no picnic.
Speaking of measure, sister website, lixcaliber.com , an introduction to the lix grid,
planetary geometric centers and the "Mother of all Scales", is where we're off to next.
It's under reconstruction, so heed your head.
These webpages are condensed and updated iterations of sites
i've produced and maintained continuously since 1996.
